• 

 

 

 

Resumão estatistica basica resumo

 

---

 

Resumão estatistica basica resumo

 

Ajude-nos a deixar-nos saber Larapedia.com relatou a um amigo / amiga ou relatar nosso site fórum sobre seu blog ou bookmarks sociais como o Facebook eTwitter, graças

 

Los siguientes textos son propiedad de sus respectivos autores y les damos las gracias por la oportunidad que nos brindan para presentar gratis a estudiantes, profesores y usuarios de la Web para sus textos ilustrativos con fines educativos y científicos.

 

 

 

La información en la medicina y la salud en este sitio es de carácter general y para propósitos informativos solamente y por lo tanto no puede sustituir en ningún caso el consejo de un médico (o una persona legalmente autorizada para la profesión).

 

 

 

 

 

Resumão estatistica basica resumo

1.   INTRODUÇÃO

ESTATÍSTICA:       ramo da matemática aplicada.

ANTIGUIDADE:      os povos já registravam o número de habitantes, nascimentos, óbitos. Faziam "estatísticas".

IDADE MÉDIA:       as informações eram tabuladas com finalidades tributárias e bélicas.

SEC. XVI:     surgem as primeiras análises sistemáticas, as primeiras tabelas e os números relativos.

SEC. XVIII:   a estatística com feição científica é batizada por GODOFREDO ACHENWALL. As tabelas ficam mais completas, surgem as primeiras representações gráficas e os cálculos de probabilidades. A estatística deixa de ser uma simples tabulação de dados numéricos para se tornar "O estudo de como se chegar a conclusão sobre uma população, partindo da observação de partes dessa população (amostra)".

 

MÉTODO ESTATÍSTICO

MÉTODO:    é um meio mais eficaz para atingir determinada meta.

MÉTODOS CIENTÍFICOS:          destacamos o método experimental e o método estatístico.

MÉTODO EXPERIMENTAL:        consiste em manter constante todas as causas, menos uma, que  sofre variação para se observar seus efeitos, caso existam.   Ex: Estudos da Química, Física, etc.

MÉTODO ESTATÍSTICO:            diante da impossibilidade de manter as causas constantes (nas ciências sociais), admitem todas essas causas presentes variando-as, registrando essas variações e procurando determinar, no resultado final, que influências cabem a cada uma delas.   Ex: Quais as causas que definem o preço de uma mercadoria quando a sua oferta diminui?

• Seria impossível, no momento da pesquisa, manter constantes a uniformidade dos salários, o gosto dos consumidores, nível geral de preços de outros produtos, etc.

 

A ESTATÍSTICA

       É uma parte da matemática aplicada que fornece métodos para coleta, organização, descrição, análise e interpretação de dados e para a utilização dos mesmos na tomada de decisões.

       A coleta, a organização ,a descrição dos dados, o cálculo e a interpretação de coeficientes pertencem à ESTATÍSTICA DESCRITIVA, enquanto a análise e a interpretação dos dados, associado a uma margem de incerteza, ficam a cargo da ESTATÍSTICA INDUTIVA ou INFERENCIAL, também chamada como a medida da incerteza ou métodos que se fundamentam na teoria da probabilidade.
.
2.  ORGANIZAÇÃO DE DADOS ESTATÍSTICOS

FASES DO MÉTODO ESTATÍSTICO

1º - DEFINIÇÃO DO PROBLEMA :        Saber exatamente aquilo que se pretende pesquisar é o mesmo que definir corretamente o problema.

2º - PLANEJAMENTO :    Como levantar informações ? Que dados deverão ser obtidos ? Qual levantamento a ser utilizado? Censitário?  Por amostragem? E o cronograma de atividades ? Os custos envolvidos ? etc.

3º - COLETA DE DADOS:           Fase operacional. É o registro sistemático de dados, com um objetivo determinado.

Dados primários:          quando são publicados pela própria pessoa ou organização que os haja recolhido.  Ex:  tabelas do censo demográfico do IBGE.

Dados secundários:               quando são publicados por outra organização. Ex: quando determinado jornal publica estatísticas referentes ao censo demográfico extraídas do IBGE.

OBS:             É mais seguro trabalhar com fontes primárias. O uso da fonte secundária traz o grande risco de erros de transcrição.

Coleta Direta:             quando é obtida diretamente da fonte. Ex: Empresa que realiza uma pesquisa para saber a preferência dos consumidores pela sua marca.

coletacontínua:          registros de nascimento, óbitos, casamentos;
coleta periódica:       recenseamento demográfico, censo industrial;
coleta ocasional:   registro de casos de dengue.
Coleta Indireta:              Éfeita por deduções a partir dos elementos conseguidos pela coleta direta, por analogia, por avaliação,indícios ou proporcionalização.

4º - APURAÇÃO DOS DADOS:                        Resumo dos dados através de sua contagem e agrupamento. É a condensação e tabulação de dados.

5º - APRESENTAÇÃO DOS DADOS:    Há duas formas de apresentação, que não se excluem mutuamente. A apresentação tabular, ou seja é uma apresentação numérica dos dados em linhas e colunas distribuídas de modo ordenado, segundo regras práticas fixadas pelo Conselho Nacional de Estatística. A apresentação gráfica dos dados numéricos constitui uma apresentação geométrica permitindo uma visão rápida e clara do fenômeno.

6º - ANÁLISE E INTERPRETAÇÃO DOS DADOS:    A última fase do trabalho estatístico é a mais importante e delicada. Está ligada essencialmente ao cálculo de medidas e coeficientes, cuja finalidade principal é descrever o fenômeno (estatística descritiva).

DEFINIÇÕES BÁSICAS DA ESTATÍSTICA
.
FENÔMENO ESTATÍSTICO:       é qualquer evento que se pretenda analisar, cujo estudo seja possível a aplicação do método estatístico. São divididos em três grupos:

Fenômenos de massa ou coletivo:                      são aqueles que não podem ser definidos por uma simples observação. A estatística dedica-se ao estudo desses fenômenos. Ex: A natalidade na Grande Vitória, O preço médio da cerveja no Espírito Santo, etc.

Fenômenos individuais:                          são aqueles que irão compor os fenômenos de massa.   Ex: cada nascimento na Grande Vitória, cada preço de cerveja no Espírito Santo, etc.

Fenômenos de multidão:                        quando as características observadas para a massa não se verificam para o particular.

DADO ESTATÍSTICO:      é um dado numérico e é considerado a matéria-prima sobre a qual iremos aplicar os métodos estatísticos.

POPULAÇÃO:        é o conjunto total de elementos portadores de, pelo menos, uma característica comum.

AMOSTRA:     é uma parcela representativa da população que é examinada com o propósito de tirarmos conclusões sobre a essa população.

PARÂMETROS:     São valores singulares que existem na população e que servem para caracterizá-la. Para definirmos um parâmetro devemos examinar toda a população.  Ex: Os alunos do 2º ano da FACEV têm em média 1,70 metros de estatura.

ESTIMATIVA:         é um valor aproximado do parâmetro e é calculado com o uso da amostra.

ATRIBUTO:    quando os dados estatísticos apresentam um caráter qualitativo, o levantamento e os estudos necessários ao tratamento desses dados são designados genericamente de estatística de atributo.

VARIÁVEL:             É o conjunto de resultados possíveis de um fenômeno.

VARIÁVEL QUALITATIVA:         Quando seu valores são expressos por atributos: sexo, cor da pele,etc.

VARIÁVEL QUANTITATIVA:      Quando os dados são de caráter nitidamente quantitativo, e o conjunto dos resultados possui uma estrutura numérica, trata-se portanto da estatística de variável e se dividem em :

VARIÁVEL DISCRETA OU DESCONTÍNUA:   Seus valores são expressos geralmente através de números inteiros não negativos.  Resulta normalmente de contagens.  Ex:  Nº de alunos presentes às aulas de introdução à estatística econômica no 1º semestre de 1997: mar = 18 , abr = 30 , mai = 35 , jun = 36.

 

VARIÁVEL CONTÍNUA:    Resulta normalmente de uma mensuração, e a escala numérica de seus possíveis valores corresponde ao conjunto R dos números Reais, ou seja, podem assumir, teoricamente, qualquer valor entre dois limites. Ex.: Quando você vai medir a temperatura de seu corpo com um termômetro de mercúrio o que ocorre é o seguinte: O filete de mercúrio, ao dilatar-se, passará por todas as temperaturas intermediárias até chegar na temperatura atual do seu corpo.

Exemplos -
. Cor dos olhos das alunas:                                                      qualitativa
. Índice de liquidez nas indústrias capixabas:                          quantitativa contínua
. Produção de café no Brasil:                                                   quantitativa contínua
. Número de defeitos em aparelhos de TV:                             quantitativa discreta
. Comprimento dos pregos produzidos por uma empresa:      quantitativa contínua
. O ponto obtido em cada jogada de um dado:                        quantitativa discreta

 

AMOSTRAGEM

MÉTODOS PROBABILÍSTICOS
       Exige que cada elemento da população possua determinada probabilidade de ser selecionado. Normalmente possuem a mesma probabilidade.  Assim, se N for o tamanho da população, a probabilidade de cada elemento ser selecionado será 1/N.  Trata-se do método que garante cientificamente a aplicação das técnicas estatísticas de inferências.  Somente com base em amostragens probabilísticas é que se podem realizar inferências ou induções sobre a população a partir do conhecimento da amostra.

• É uma técnica especial para recolher amostras, que garantem, tanto quanto possível, o acaso na escolha.

 

.
AMOSTRAGEM CASUAL ou  ALEATÓRIA SIMPLES
       É o processo mais elementar e freqüentemente utilizado. É equivalente a um sorteio lotérico.  Pode ser realizada numerando-se a população de 1 a n e sorteando-se, a seguir, por meio de um dispositivo aleatório qualquer, x números dessa seqüência, os quais corresponderão aos elementos pertencentes à amostra.

Ex:      Vamos obter uma amostra, de 10%, representativa para a pesquisa da estatura de 90 alunos de uma escola:
1º - numeramos os alunos de 1 a 90.
2º - escrevemos os números dos alunos, de 1 a 90, em pedaços iguais de papel, colocamos na urna e após mistura retiramos, um a um, nove números que formarão a amostra.
OBS: quando o número de elementos da amostra é muito grande, esse tipo de sorteio torna-se muito trabalhoso. Neste caso utiliza-se uma Tabela de números aleatórios, construída de modo que os algarismos de 0 a 9 são distribuídos ao acaso nas linhas e colunas.
.

 

.AMOSTRAGEM PROPORCIONAL ESTRATIFICADA:
       Quando a população se divide em estratos (sub-populações), convém que o sorteio dos elementos da amostra leve em consideração tais estratos, daí obtemos os elementos da amostra proporcional ao número de elementos desses estratos.
Ex:  Vamos obter uma amostra proporcional estratificada, de 10%, do exemplo anterior, supondo, que, dos 90 alunos, 54 sejam meninos e 36 sejam meninas. São portanto dois estratos (sexo masculino e sexo feminino). Logo, temos:

Numeramos então os alunos de 01 a 90, sendo 01 a 54 meninos e 55 a 90, meninas e procedemos o sorteio casual com urna ou tabela de números aleatórios.
.

AMOSTRAGEM SISTEMÁTICA:
       Quando os elementos da população já se acham ordenados, não há necessidade de construir o sistema de referência. São exemplos os prontuários médicos de um hospital, os prédios de uma rua, etc. Nestes casos, a seleção dos elementos que constituirão a amostra pode ser feita por um sistema imposto pelo pesquisador.

Ex: Suponhamos uma rua com 900 casas, das quais desejamos obter uma amostra formada por 50 casas para uma pesquisa de opinião. Podemos, neste caso, usar o seguinte procedimento:  como 900/50 = 18, escolhemos por sorteio casual um número de 01 a 18, o qual indicaria o primeiro elemento sorteado para a amostra; os demais elementos seriam periodicamente considerados de 18 em 18. Assim, suponhamos que o número sorteado fosse 4 a amostra seria: 4ª casa, 22ª casa, 40ª casa, 58ª casa, 76ª casa, etc.
  

AMOSTRAGEM POR CONGLOMERADOS (ou AGRUPAMENTOS)
       Algumas populações não permitem, ou tornam extremamente difícil que se identifiquem seus elementos. Não obstante isso, pode ser relativamente fácil identificar alguns subgrupos da população.  Em tais casos, uma amostra aleatória simples desses subgrupos (conglomerados) pode se colhida, e uma contagem completa deve ser feita para o conglomerado sorteado. Agrupamentos típicos são quarteirões, famílias, organizações, agências, edifícios etc.

Ex:  Num levantamento da população de determinada cidade, podemos dispor do mapa indicando cada quarteirão e não dispor de uma relação atualizada dos seus moradores. Pode-se, então, colher uma amostra dos quarteirões e fazer a contagem completa de todos os que residem naqueles quarteirões sorteados.

 

MÉTODOS NÃO PROBABILÍSITCOS
       São amostragens em que há uma escolha deliberada dos elementos da amostra. Não é possível generalizar os resultados das pesquisas para a população, pois as amostras não-probabilísticas não garantem a representatividade da população.

 

AMOSTRAGEM ACIDENTAL
       Trata-se de uma amostra formada por aqueles elementos que vão aparecendo, que são possíveis de se obter até completar o número de elementos da amostra. Geralmente utilizada em pesquisas de opinião, em que os entrevistados são acidentalmente escolhidos.

Ex: Pesquisas de opinião em praças públicas, ruas de grandes cidades;

 

AMOSTRAGEM INTENCIONAL
       De acordo com determinado critério, é escolhido intencionalmente um grupo de elementos que irão compor a amostra. O investigador se dirige intencionalmente a grupos de elementos dos quais deseja saber a opinião.

Ex:  Numa pesquisa sobre preferência por determinado cosmético, o pesquisador se dirige a um grande salão de beleza e entrevista as pessoas que ali se encontram.

 

AMOSTRAGEM POR QUOTAS
       Um dos métodos de amostragem mais comumente usados em levantamentos de mercado e em prévias eleitorais. Ele abrange três fases:

1ª - classificação da população em termos de propriedades que se sabe, ou presume, serem relevantes para a característica a ser estudada;

2ª - determinação da proporção da população para cada característica, com base na constituição conhecida, presumida ou estimada, da população;

3ª - fixação de quotas para cada entrevistador a quem tocará a responsabilidade de selecionar entrevistados, de modo que a amostra total observada ou entrevistada contenha a proporção e cada classe tal como determinada na 2ª fase.

Ex:      Numa pesquisa sobre o "trabalho das mulheres na atualidade", provavelmente se terá interesse em considerar: a divisão cidade e campo, a habitação, o número de filhos, a idade dos filhos, a renda média, as faixas etárias etc.
A primeira tarefa é descobrir as proporções (porcentagens) dessas características na população. Imagina-se que haja 47% de homens e 53% de mulheres na população. Logo, uma amostra de 50 pessoas deverá ter 23 homens e 27 mulheres. Então o pesquisador receberá uma "quota" para entrevistar 27 mulheres. A consideração de várias categorias exigirá uma composição amostral que atenda ao n determinado e às proporções populacionais estipuladas.
.

 

SÉRIES ESTATÍSTICAS

TABELA:      É um quadro que resume um conjunto de dados dispostos segundo linhas e colunas de maneira sistemática.

• De acordo com a Resolução 886 do IBGE, nas casas ou células da tabela devemos colocar :

• um traço horizontal ( - ) quando o valor é zero;
• três pontos ( ... ) quando não temos os dados;
• zero ( 0 ) quando o valor é muito pequeno para ser expresso pela unidade utilizada;
• um ponto de interrogação ( ? ) quando temos dúvida quanto à exatidão de determinado valor.

Obs: O lado direito e esquerdo de uma tabela oficial deve ser aberto..

 

SÉRIE ESTATÍSTICA:      É qualquer tabela que apresenta a distribuição de um conjunto de dados estatísticos em função da época, do local ou da espécie.

 

Séries Homógradas:            são aquelas em que a variável descrita apresenta variação discreta ou descontínua. Podem ser do tipo temporal, geográfica ou específica.

a) Série Temporal:          Identifica-se pelo caráter variável do fator cronológico. O local e a espécie (fenômeno) são elementos fixos. Esta série também é chamada de histórica ou evolutiva.

  ABC VEÍCULOS LTDA.
Vendas no 1º bimestre de 1996

.
b) Série Geográfica:               Apresenta como elemento variável o fator geográfico. A época e o fato (espécie) são elementos fixos. Também é chamada de espacial, territorial ou de localização.

ABC VEÍCULOS LTDA.
Vendas no 1º bimestre de 1996

c) Série Específica:                O caráter variável é apenas o fato ou espécie. Também é chamada de série categórica.

ABC VEÍCULOS LTDA.
Vendas no 1º bimestre de 1996

 

SÉRIES CONJUGADAS:     Também chamadas de tabelas de dupla entrada. São apropriadas à apresentação de duas ou mais séries de maneira conjugada, havendo duas ordens de classificação: uma horizontal e outra vertical. O exemplo abaixo é de uma série geográfica-temporal.

ABC VEÍCULOS LTDA.
Vendas no 1º bimestre de 1996

GRÁFICOS ESTATÍSTICOSG

       São representações visuais dos dados estatísticos que devem corresponder, mas nunca substituir as tabelas estatísticas.

Características:       Uso de escalas, sistema de coordenadas, simplicidade, clareza e veracidade.

Gráficos de informação:                    São gráficos destinados principalmente ao público em geral, objetivando proporcionar uma visualização rápida e clara. São gráficos tipicamente expositivos, dispensando comentários explicativos adicionais. As legendas podem ser omitidas, desde que as informações desejadas estejam presentes.

 

Gráficos de análise:                São gráficos que prestam-se melhor ao trabalho estatístico, fornecendo elementos úteis à fase de análise dos dados, sem deixar de ser também informativos. Os gráficos de análise freqüentemente vêm acompanhados de uma tabela estatística. Inclui-se, muitas vezes um texto explicativo, chamando a atenção do leitor para os pontos principais revelados pelo gráfico.

 

• Uso indevido de Gráficos: Podem trazer uma idéia falsa dos dados que estão sendo analisados, chegando mesmo a confundir o leitor. Trata-se, na realidade, de um problema de construção de escalas.

.
Classificação dos gráficos:        Diagramas, Estereogramas, Pictogramas e Cartogramas.
.
1 - Diagramas:
       São gráficos geométricos dispostos em duas dimensões. São os mais usados na representação de séries estatísticas. Eles podem ser :

• Gráficos em barras horizontais.

 

1.2-     Gráficos em barras verticais ( colunas ).

• Quando as legendas não são breves usa-se de preferência os gráficos em barras horizontais. Nesses gráficos os retângulos têm a mesma base e as alturas são proporcionais aos respectivos dados.
• A ordem a ser observada é a cronológica, se a série for histórica, e a
• decrescente, se for geográfica ou categórica.

• Gráficos em barras compostas.

 

1.4-     Gráficos em colunas superpostas.

• Eles diferem dos gráficos em barras ou colunas convencionais apenas pelo fato de apresentar cada barra ou coluna segmentada em partes componentes. Servem para representar comparativamente dois ou mais atributos.

1.5-     Gráficos em linhas ou lineares.

• São freqüentemente usados para representação de séries cronológicas com um grande número de períodos de tempo. As linhas são mais eficientes do que as colunas, quando existem intensas flutuações nas séries ou quando há necessidade de se representarem várias séries em um mesmo gráfico.

• Quando representamos, em um mesmo sistema de coordenadas, a variação de dois fenômenos, a parte interna da figura formada pelos gráficos desses fenômenos é denominada de área de excesso.

 

1.5-     Gráficos em setores.

• Este gráfico é construído com base em um círculo, e é empregado sempre que desejamos ressaltar a participação do dado no total. O total é representado pelo círculo, que fica dividido em tantos setores quantas são as partes. Os setores são tais que suas áreas são respectivamente proporcionais aos dados da série. O gráfico em setores só deve ser empregado quando há, no máximo, sete dados.

• Obs:  As séries temporais geralmente não são representadas por este tipo de gráfico.

 

.
2 - Estereogramas:
       São gráficos geométricos dispostos em três dimensões, pois representam volume. São usados nas representações gráficas das tabelas de dupla entrada. Em alguns casos este tipo de gráfico fica difícil de ser interpretado dada a pequena precisão que oferecem.
.
3 - Pictogramas:
       São construídos a partir de figuras representativas da intensidade do fenômeno. Este tipo de gráfico tem a vantagem de despertar a atenção do público leigo, pois sua forma é atraente e sugestiva. Os símbolos devem ser auto-explicativos. A desvantagem dos pictogramas é que apenas mostram uma visão geral do fenômeno, e não de detalhes minuciosos. Veja o exemplo abaixo:

4- Cartogramas:
       São ilustrações relativas a cartas geográficas (mapas). O objetivo desse gráfico é o de figurar os dados estatísticos diretamente relacionados com áreas geográficas ou políticas.

 

DISTRIBUIÇÃO DE FREQÜÊNCIA
       É um tipo de tabela que condensa uma coleção de dados conforme as freqüências (repetições de seus valores).

Tabela primitiva ou dados brutos:                      É uma tabela ou relação de elementos que não foram numericamente organizados. É difícil formarmos uma idéia exata do comportamento do grupo como um todo, a partir de dados não ordenados.

Ex : 45, 41, 42, 41, 42 43, 44, 41 ,50, 46, 50, 46, 60, 54, 52, 58, 57, 58, 60, 51

ROL:                  É a tabela obtida após a ordenação dos dados (crescente ou decrescente).

Ex : 41, 41, 41, 42, 42 43, 44, 45 ,46, 46, 50, 50, 51, 52, 54, 57, 58, 58, 60, 60

Distribuição de freqüência sem intervalos de classe:    É a simples condensação dos dados conforme as repetições de seu valores. Para um ROL de tamanho razoável esta distribuição de freqüência é inconveniente, já que exige muito espaço. Veja exemplo abaixo:

Distribuição de freqüência com intervalos de classe:Quando o tamanho da amostra é elevado, é mais racional efetuar o agrupamento dos valores em vários intervalos de classe.

 

ELEMENTOS DE UMA DISTRIBUIÇÃO DE FREQÜÊNCIA (com intervalos de classe)

 
CLASSE:      são os intervalos de variação da variável e é simbolizada por  i  e o número total de classes simbolizada por k. Ex: na tabela anterior k = 5 e  49 |------- 53 é a 3ª classe, onde i = 3.

 

LIMITES DE CLASSE:      são os extremos de cada classe. O menor número é o limite inferior de classe ( li ) e o maior número, limite superior de classe ( Li ).  Ex: em 49 |------- 53,... l3 = 49 e L3 = 53.  O símbolo |------- representa um intervalo fechado à esquerda e aberto à direita. O dado 53 do ROL não pertence a classe 3 e sim a classe 4 representada por 53 |------- 57.

AMPLITUDE DO INTERVALO DE CLASSE:      é obtida através da diferença entre o limite superior e inferior da classe e é simbolizada por hi = Li - li.   Ex: na tabela anterior hi = 53 - 49 = 4. Obs: Na distribuição de freqüência c/ classe o hi será igual em todas as classes.

 

AMPLITUDE TOTAL DA DISTRIBUIÇÃO:       é a diferença entre o limite superior da última classe e o limite inferior da primeira classe.AT = L(max) - l(min).   Ex: na tabela anterior AT = 61 - 41= 20.

 

AMPLITUDE TOTAL DA AMOSTRA (ROL):   é a diferença entre o valor máximo e o valor mínimo da amostra (ROL). Onde AA = Xmax - Xmin.   Em nosso exemplo AA = 60 - 41 = 19.
Obs:   AT sempre será maior que AA.

 

PONTO  MÉDIO DE CLASSE:     é o ponto que divide o intervalo de classe em duas partes iguais. .......Ex: em 49 |------- 53 o ponto médio x3 = (53+49)/2 = 51, ou seja  x3=( l3 + L3 )/2.

 

Método prático para construção de uma Distribuição de Freqüências c/ Classe

1º -     Organize os dados brutos em um ROL.

2º -     Calcule a amplitude amostral AA.

• No nosso exmplo:   AA  = 60 - 41  = 19

3º -     Calcule o número de classes através da "Regra de Sturges":

Obs:   Qualquer regra para determinação do nº de classes da tabela não nos levam a uma decisão final; esta vai depender, na realidade de um julgamento pessoal, que deve estar ligado à natureza dos dados.

No nosso exemplo:   n  =  20 dados, então ,a princípio, a regra sugere a adoção de 5 classes.

4º -     Decidido o nº de classes, calcule então a amplitude do intervalo de classeh > AA / i.
No nosso exemplo: AA/i = 19/5 = 3,8 . Obs: Como h > AA/i um valor ligeiramente superior para haver folga na última classe. Utilizaremos então  h = 4

5º -     Temos então o menor nº da amostra, o nº de classes e a amplitude do intervalo. Podemos montar a tabela, com o cuidado para não aparecer classes com freqüência = 0 (zero).
No nosso exemplo: o menor nº da amostra = 41 + h = 45, logo a primeira classe será representada por ...... 41 |------- 45. As classes seguintes respeitarão o mesmo procedimento.
O primeiro elemento das classes seguintes sempre serão formadas pelo último elemento da classe anterior.

 

REPRESENTAÇÃO GRÁFICA DE UMA DISTRIBUIÇÃO

Histograma,  Polígono de freqüência e  Polígono de freqüência acumulada

       Em todos os gráficos acima utilizamos o primeiro quadrante do sistema de eixos coordenados cartesianos ortogonais. Na linha horizontal (eixo das abscissas) colocamos os valores da variável e na linha vertical (eixo das ordenadas), as freqüências.
.
Histograma:           é formado por um conjunto de retângulos justapostos, cujas bases se localizam sobre o eixo horizontal, de tal modo que seus pontos médios coincidam com os pontos médios dos intervalos de classe. A área de um histograma é proporcional à soma das freqüências simples ou absolutas.
Freqüências simples ou absoluta:                  são os valores que realmente representam o número de dados de cada classe. A soma das freqüências simples é igual ao número total dos dados da distribuição.

 

Freqüências relativas:            são os valores das razões entre as freqüência absolutas de cada classe e a freqüência total da distribuição. A soma das freqüências relativas é igual a 1 (100 %).
.

Polígono de freqüência:     é um gráfico em linha, sendo as freqüências marcadas sobre perpendiculares ao eixo horizontal, levantadas pelos pontos médios dos intervalos de classe. Para realmente obtermos um polígono (linha fechada), devemos completar a figura, ligando os extremos da linha obtida aos pontos médios da classe anterior à primeira e da posterior à última, da distribuição.
.

Polígono de freqüência acumulada:    é traçado marcando-se as freqüências acumuladas sobre perpendiculares ao eixo horizontal, levantadas nos pontos correspondentes aos limites superiores dos intervalos de classe.

 

Freqüência simples acumulada de uma classe:                           é o total das freqüências de todos os valores inferiores ao limite superior do intervalo de uma determinada classe.

 

Freqüência relativa acumulada de um classe:                              é a freqüência acumulada da classe, dividida pela freqüência total da distribuição.

 

fi = freqüência simples;    xi = ponto médio de classe;    fri = freqüência simples acumulada;
Fi = freqüência relativa  e  Fri = freqüência relativa acumulada.

• Obs: uma distribuição de freqüência sem intervalos de classe é representada graficamente por um diagrama onde cada valor da variável é representado por um segmento de reta vertical e de comprimento proporcional à respectiva freqüência.

3.   MEDIDAS DE POSIÇÃO

Introdução
       São as estatísticas que representam uma série de dados orientando-nos quanto à posição da distribuição em relação ao eixo horizontal do gráfico da curva de freqüência.

• As medidas de posições mais importantes são as medidas de tendência central ou promédias (verifica-se uma tendência dos dados observados a se agruparem em torno dos valores centrais).

 

• As medidas de tendência central mais utilizadas são: média aritmética, moda e mediana. Outros promédios menos usados são as médias: geométrica, harmônica, quadrática, cúbica e biquadrática.

• As outras medidas de posição são as separatrizes, que englobam: a própria mediana, os decis, os quartis e os percentis.

.

 

MÉDIA ARITMÉTICA =

       É igual ao quociente entre a soma dos valores do conjunto e o número total dos valores.
 

......

onde  xi são os valores da variável e n o número de valores.
.

Dados não-agrupados:              Quando desejamos conhecer a média dos dados não-agrupados em tabelas de freqüências, determinamos a média aritmética simples.

 

Ex:      Sabendo-se que a venda diária de arroz tipo A, durante uma semana, foi de 10, 14, 13, 15, 16, 18 e 12 kilos, temos, para venda média diária na semana de:
.= (10+14+13+15+16+18+12) / 7 = 14 kilos

 

Desvio em relação à média:       é a diferença entre cada elemento de um conjunto de valores e a média aritmética, ou seja:.
 

. di = Xi -

 

No exemplo anterior temos sete desvios:...   d1 = 10 - 14 = - 4 , ...d2 = 14 - 14 = 0 ,   d3 = 13 - 14 = - 1 , ...d4 = 15 - 14 = 1 ,... d5 = 16 - 14 = 2 ,... d6 = 18 - 14 = 4 ...e.  ..   d7 = 12 - 14 = - 2.
.

 

Propriedades da média aritmética 

 

1ª propriedade:      A soma algébrica dos desvios em relação à média é nula.

• No exemplo anterior : d1+d2+d3+d4+d5+d6+d7 = 0

 

2ª propriedade:      Somando-se (ou subtraindo-se) uma constante (c) a todos os valores de uma variável, a média do conjunto fica aumentada ( ou diminuída) dessa constante.

• Se no exemplo original somarmos a constante 2 a cada um dos valores da variável temos:

 

Y = 12+16+15+17+18+20+14 / 7 = 16 kilos ou
Y = .+ 2 = 14 +2 = 16 kilos

 

3ª propriedade:      Multiplicando-se (ou dividindo-se) todos os valores de uma variável por uma constante (c), a média do conjunto fica multiplicada ( ou dividida) por essa constante.

• Se no exemplo original multiplicarmos a constante 3 a cada um dos valores da variável temos:

 

Y = 30+42+39+45+48+54+36 / 7 = 42 kilos ou
Y = x 3 = 14 x 3 = 42 kilos

 

.
Dados agrupados:

Sem intervalos de classe       Consideremos a distribuição relativa a 34 famílias de quatro filhos, tomando para variável o número de filhos do sexo masculino. Calcularemos a quantidade média de meninos por família:

• Como as freqüências são números indicadores da intensidade de cada valor da variável, elas funcionam como fatores de ponderação, o que nos leva a calcular a média aritmética ponderada, dada pela fórmula:

 

onde 78 / 34  =  2,3 meninos por família
Com intervalos de classe       Neste caso, convencionamos que todos os valores incluídos em um determinado intervalo de classe coincidem com o seu ponto médio, e determinamos a média aritmética ponderada por meio da fórmula:
 

..

onde Xi é o ponto médio da classe.

Ex: Calcular a estatura média de bebês conforme a tabela abaixo.

Aplicando a fórmula acima temos: 2.440 / 40.= 61. logo... = 61 cm

Média Geométrica  =  g

       É a raiz n-ésima do produto de todos eles.

Média Geométrica Simples:

Ex.: - Calcular a média geométrica dos seguintes conjuntos de números:E

a) { 10, 60, 360 }.:                 = ( 10  * 60 * 36 0) ^ (1/3) ....R: 60
b) { 2, 2, 2 }........:                 = (2 * 2 * 2 ^ (1/3) ..     .R: 2
c) { 1, 4, 16, 64 }:                = (1 * 4 * 16 * 64  ) ^(1/4) ....R: 8
.

Média Geométrica Ponderada :

 
Ex - Calcular a média geométrica dos valores da tabela abaixo:

...xi...	...fi...
1	2
3	4
9	2
27	1
Total	9

=    (12 * 34 * 92 * 271) (1/9)........R: 3,8296

 

.
MÉDIA HARMÔNICA  - h

       É o inverso da média aritmética dos inversos.
.
Média Harmônica Simples:.  (para dados não agrupados)

..

 

.
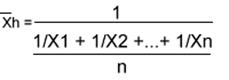
Média Harmônica Ponderada :  (para dados agrupados em tabelas de freqüências)
 

..

 

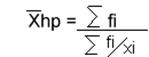Ex.: Calcular a média harmônica dos valores da tabela abaixo:

classes	....fi....	....xi....	........fi/xi........
1 |--------- 3	2	2	2/2 = 1,00
3 |--------- 5	4	4	4/4 = 1,00
5 |--------- 7	8	6	8/6 = 1,33
7 |--------- 9	4	8	4/8 = 0,50
9 |--------- 11	2	10	2/10 = 0,20
total	20		4,03

Resp: 20 / 4,03 = 4,96

OBS:       A média harmônica não aceita valores iguais a zero como dados de uma série.

• A igualdade ....só ocorrerá quando todos os valores da série forem iguais.

 

OBS:       Quando os valores da variável não forem muito diferentes, verifica-se aproximadamente a seguinte relação:

 

h ) /.2

 

• Demonstraremos a relação acima com os seguintes dados:

z = { 10,1 ; 10,1 ; 10,2 ; 10,4 ; 10,5 }

Média aritmética = 51,3 / 5           = 10,2600
Média geométrica=                                  = 10,2587

Média harmônica = 5 / 0,4874508           = 10,2574

Comprovando a relação: 10,2600 + 10,2574 / 2 = 10,2587 = média geométrica
.

 

MODA  -  Mo

       É o valor que ocorre com maior freqüência em uma série de valores.

• Desse modo, o salário modal dos empregados de uma fábrica é o salário mais comum, isto é, o salário recebido pelo maior número de empregados dessa fábrica.

 

Fonte do documento:http://www.portalprudente.com.br/apostilas/Estat%EDstica/estatistica.doc

Site para visitar: http://www.portalprudente.com.br/

Autor do texto: não especificado no documento de origem ou indicadas no texto

Google Palavras-chave: Resumão estatistica basica resumo Tipo de Arquivo: doc

Se você é o autor do texto acima e concorda em não partilhar o seu conhecimento para o ensino, pesquisa, bolsas de estudo (para uso justo, como mostrado acima, nos Estados Unidos copyrigh baixa "for fair use as indicated in the United States copyrigh low"), envie um e-mail conosco e nós vamos remover o texto rapidamente.

 

Resumão estatistica basica resumo

 

Se você quer encontrar rapidamente as páginas relacionadas a um tópico específico, como xx usando o seguinte motor de busca:

 

 

 

 

Visite a página principal

 

 

 

 

Resumão estatistica basica resumo

 

 

Por favor, visite índice inicial de todos os temas, graças

 

Termos de uso ea política de privacidade e condições de utilização

 

 

 

Resumão estatistica basica resumo